EmmmuaCode
wufan
2022-12-29
目录

排序算法

# 排序算法

# 排序算法的介绍

排序也称排序算法(Sort Algorithm)，排序是将一组数据，依指定的顺序进行排列的过程。

# 排序的分类

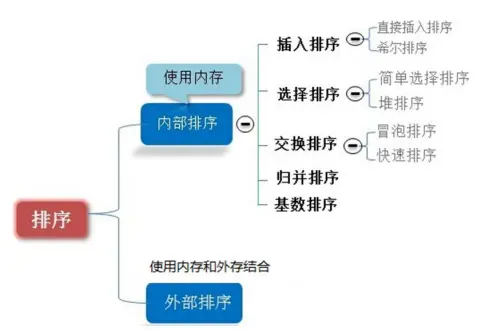
  1. 内部排序

    指将需要处理的所有数据都加载到内部存储器(内存)中进行排序。

  2. 外部排序法

    数据量过大，无法全部加载到内存中，需要借助**外部存储(文件等)**进行排序。

  3. 常见的排序算法分类

image

# 算法的时间复杂度

# 度量一个程序(算法)执行时间的两种方法

  1. 事后统计的方法

    这种方法可行,但是有两个问题:一是要想对设计的算法的运行性能进行评测，需要实际运行该程序;二是所得时间的统计量依赖于计算机的硬件、软件等环境因素,这种方式，要在同一台计算机的相同状态下运行，才能比较那个算法速度更快。

  2. 事前估算的方法

    通过分析某个算法的时间复杂度来判断哪个算法更优.

# 时间频度

  • 基本介绍

    时间频度:一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

  • 举例说明-基本案例

    比如计算.1-100所有数字之和，我们设计两种算法:

image

  • 举例说明-忽略常数项

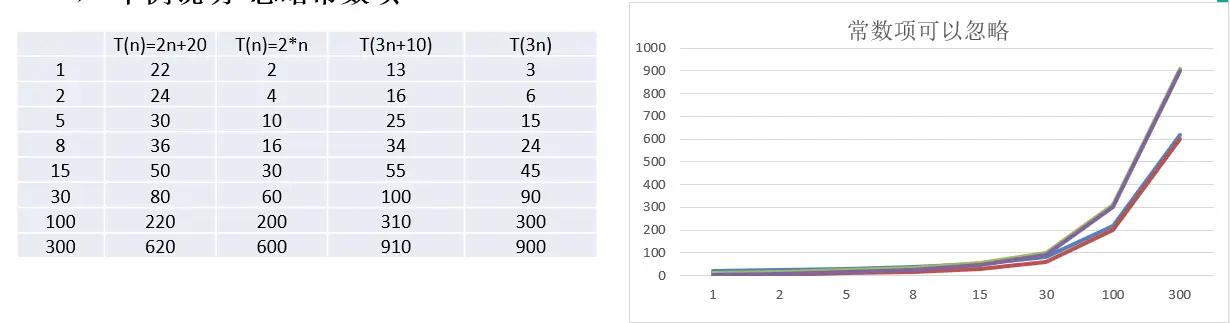
image

结论：

  1. 2n+20 和 2n 随着 n 变大，执行曲线无限接近, 20 可以忽略
  2. 3n+10 和 3n 随着 n 变大，执行曲线无限接近, 10 可以忽略
  • 举例说明-忽略低次项

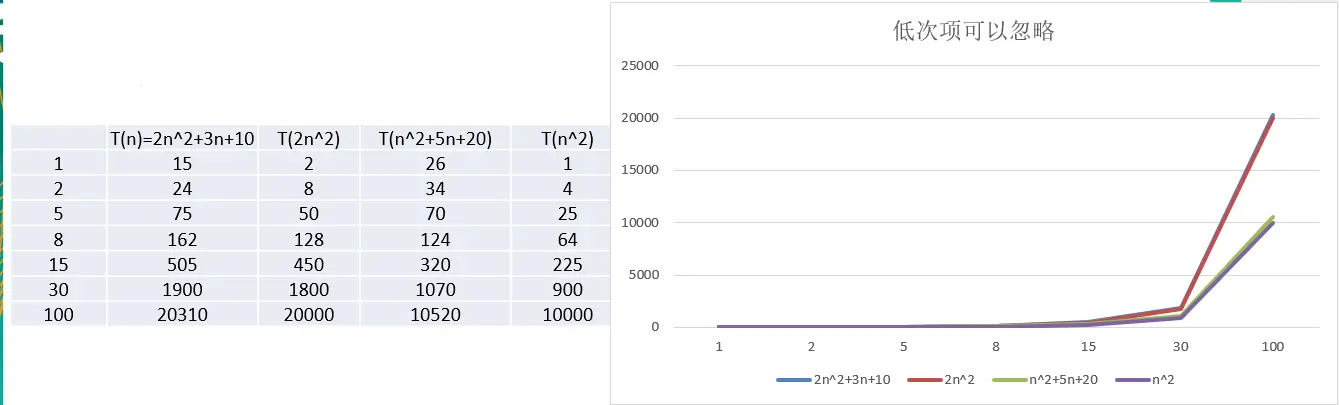
image

结论：

  1. 2n2+3n+10 和 2n2 随着 n 变大，执行曲线无限接近，可以忽略 3n+10
  2. n2+5n+20 和 n2 随着 n 变大，执行曲线无限接近，可以忽略 5n+20
  • 举例说明-忽略系数

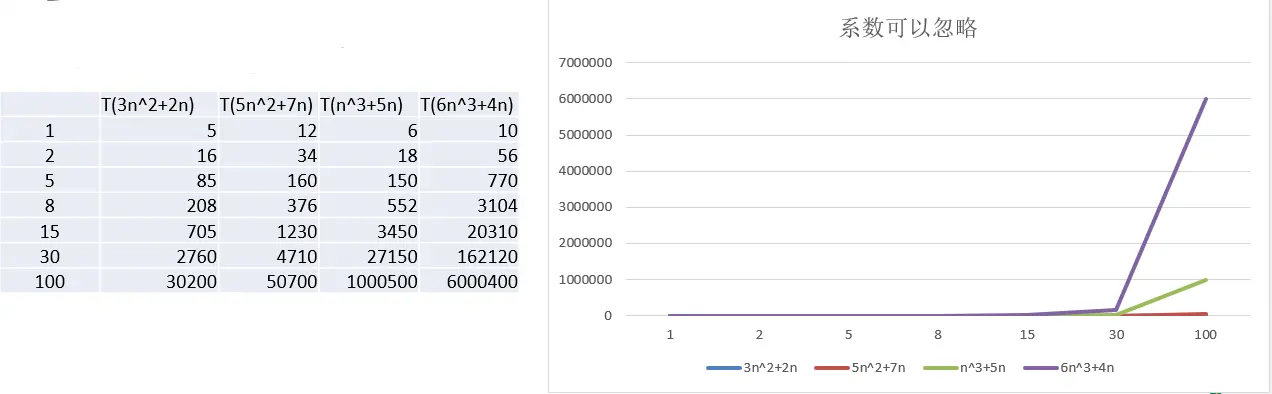
image

结论：

  1. 随着 n 值变大，5n2+7n 和 3n2+2n，执行曲线重合，说明这种情况下，5 和 3 可以省略。
  2. 而 n3+5n 和 6n3+4n，执行曲线分离，说明多少次方式关键。

# 时间复杂度

  1. 一般情况下，算法中的基本操作语句的重复执行次数是问题规模n的某个函数，用 T(n) 表示，若有某个辅助函数 f(n) ，使得当 n 趋近于无穷大时，T(n)/ f(n)的极限值为不等于零的常数，则称 f(n)是 T(n)的同数量级函数。记作 T(n)=O( f(n)) ，称 o( f((n)) 为算法的渐进时间复杂度，简称时间复杂度。
  2. T(n) 不同，但时间复杂度可能相同。如: T(n)=n2+7n+6 与 T(n)=3n2+2n+2 它们的T(n)不同，但时间复杂度相同，都为O(n2)。
  3. 计算时间复杂度的方法：
    • 用常数Ⅰ代替运行时间中的所有加法常数‘T(n)=n2+7n+6 => T(n)=n2+7n+1
    • 修改后的运行次数函数中，只保留最高阶项T(n)=n2+7n+1 => T(n)= n2
    • 去除最高阶项的系数‘T(n)= n2 => T(n)= n2  => O(n2)

# 常见的时间复杂度

  1. 常数阶 O(1)
  2. 对数阶 O(log2n)
  3. 线性阶 O(n)
  4. 线性对数阶 O(nlog2n)
  5. 平方阶 O(n2)
  6. 立方阶 O(n3)
  7. k 次方阶 O(nk)
  8. 指数阶 O(22)

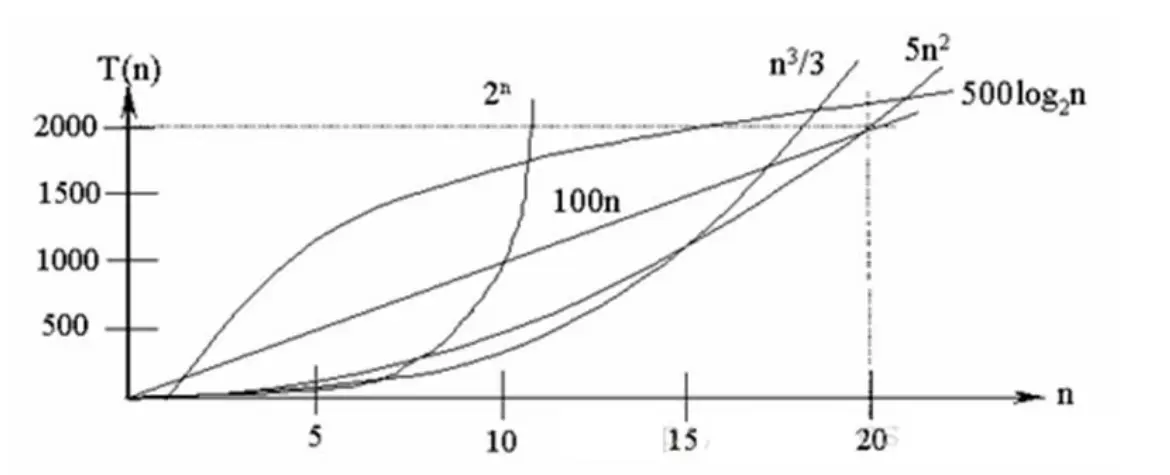
常见的时间复杂度对应的图： image

说明：

  1. 常见的算法时间复杂度由小到大依次为：O(1)<O(log2n)<O(n)<O(n2)<O(n3)<O(nk)<O(2n)，随着问题规模 n 的不断增大，上述时间复杂度不断增大，算法的执行效率越低
  2. 从图中可见，我们应该尽可能避免使用指数阶的算法

常数阶 O(1)

无论代码执行了多少行，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是O(1)

int i = 1;
int j = 2;
++i;
j++;
int m = i + j;
1
2
3
4
5

上述代码在执行的时候，它消耗的时候并不随着某个变量的增长而增长，那么无论这类代码有多长，即使有几万几十万行，都可以用O(1)来表示它的时间复杂度。

对数阶 O(log2n)

int i = 1;
while(i < n){
    i = i * 2;
}
1
2
3
4

说明:在while循环里面，每次都将 i 乘以 2 ，乘完之后，i 距离 n 就越来越近了。假设循环 x 次之后，i 就大于 2 了，此时这个循环就退出了，也就是说 2 的 x 次方等于 n ，那么x=logzn也就是说当循环 log2n 次以后，这个代码就结束了。因此这个代码的时间复杂度为: O(log2n)。O(log2n) 的这个2时间上是根据代码变化的，i=i*3，则是O(log3n).

image

线性阶 O(n)

for(i = 1;i <= n; ++i) {
    j = 1;
    j++;
}
1
2
3
4

说明:这段代码，for 循环里面的代码会执行 n 遍，因此它消耗的时间是随着 n 的变化而变化的，因此这类代码都可以用 O(n) 来表示它的时间复杂度

线性对数阶 O(nlogN)

for(m = 1;m < n;m++) {
    i = 1;
    while(i < n) {
        i = i * 2;
    }
}
1
2
3
4
5
6

说明:线性对数阶 O(nlogN) 其实非常容易理解，将时间复杂度为O(logn)的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)，也就是了o(nlogN)

平方阶 O(n2)

for(x = 1;i <= n;x++) {
    for(i = 1;i <= n;i++) {
        j = 1;
        j++;
    }
}
1
2
3
4
5
6

说明:平方阶 O(n2) 就更容易理解了，如果把 O(n) 的代码再嵌套循环一遍，它的时间复杂度就是 O(n2)，这段代码其实就是嵌套了2层 n 循环，它的时间复杂度就是 O(n*n)， 即**O(n2)**如果将其中一层循环的 n 改成 m ，那它的时间复杂度就变成了 O(m*n)

立方阶O(n³)、K次方阶O(nk)

# 平均时间复杂度和最坏时间复杂度

  1. 平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下，该算法的运行时间。
  2. 最坏情况下的时间复杂度称最坏时间复杂度。一般讨论的时间复杂度均是最坏情况下的时间复杂度。这样做的原因是:最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限，这就保证了算法的运行时间不会比最坏情况更长。
  3. 平均时间复杂度和最坏时间复杂度是否一致，和算法有关(如图:)。

image

# 算法的空间复杂度简介

# 基本介绍

  1. 类似于时间复杂度的讨论，一个算法的空间复杂度(Space Complexity)定义为该算法所耗费的存储空间，它也是问题规模n的函数。
  2. 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如快速排序和归并排序算法，基数排序就属于这种情况
  3. 在做算法分析时，主要讨论的是时间复杂度。从用户使用体验上看，更看重的程序执行的速度。一些缓存产品(redis, memcache)和算法(基数排序)本质就是用空间换时间.

# 冒泡排序

# 基本介绍

冒泡排序(Bubble Sorting)的基本思想是:通过对待排序序列从前向后（从下标较小的元素开始〉,依次比较相邻元素的值，若发现逆序则交换，使值较大的元素逐渐从前移向后部，就象水底下的气泡一样逐渐向上冒。

优化:

因为排序的过程中，各元素不断接近自己的位置，如果一趟比较下来没有进行过交换，就说明序列有序，因此要在排序过程中设置一个标志 flag 判断元素是否进行过交换。从而减少不必要的比较。(这里说的优化，可以在冒泡排序写好后，在进行)

# 演示冒泡过程的例子

原始数组：3,9,-1,10,20

第一趟排序

(1) 3,9,-1,10,20 //如果相邻的元素逆序就交换

(2) 3,-1,9,10,20

(3) 3,-1,9,10,20

(4) 3,-1,9,10,20

第二趟排序

(1) -1,3,9,10,20

(2) -1,3,9,10,20

(3) -1,3,9,10,20

第三趟排序

(1) -1,3,9,10,20

(2) -1,3,9,10,20

第四趟排序

(2) -1,3,9,10,20

小结上面的排序过程：

  1. 一共进行数组的大小-1次大的循环。
  2. 每一趟排序的次数在逐渐的减少。
  3. 如果我们发现在某趟排序中，没有发生一次交换，可以提前结束冒泡排序。这个就是优化。

# 代码实现

我们举一个具体的案例来说明冒泡法。我们将五个无序的数: 3,9,-1,10,-2使用冒泡排序法将其排成一个从小到大的有序数列。

/**
 * @author frx
 * @version 1.0
 * @date 2022/12/30  20:22
 * desc:冒泡排序
 */
public class BubbleSort {
    public static void main(String[] args) {
        int arr[] = {3, 9, -1, 10, -2};
        System.out.println("排序前：");
        System.out.println(Arrays.toString(arr));
        bubbleSort(arr);
        System.out.println("排序后：");
        System.out.println(Arrays.toString(arr));

        //测试一下冒泡排序的速度,给80000个数据
        //创建要给80000个随机的数组
        int[] array = new int[80000];
        for (int i = 0; i < 80000; i++) {
            array[i] = (int) (Math.random() * 8000000); //生成一个[0,8000000)数
        }
        Date date1 = new Date();
        SimpleDateFormat dateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        String startTime = dateFormat.format(date1);
        System.out.println("排序前的时间=：" + startTime);

        //测试冒泡排序
        bubbleSort(array);
        Date date2 = new Date();
        String endTime = dateFormat.format(date2);
        System.out.println("排序后的时间=：" + endTime);


        //1.第一趟排序，就是将最大的数排在最后
        /*int temp = 0; //临时变量
        for (int i = 0; i < arr.length - 1; i++) {
            //如果前面的数比后面的数大，刚交换
            if (arr[i] > arr[i + 1]) {
                temp = arr[i];
                arr[i] = arr[i + 1];
                arr[i + 1] = temp;
            }
        }
        System.out.println("第一趟排序后的数组："); //[3, -1, 9, -2, 10]
        System.out.println(Arrays.toString(arr));

        // 第二趟排序，就是将最二大的数排在最后，比较次数减一，因为最大数已经确定
        for (int i = 0; i < arr.length - 1 - 1; i++) {
            //如果前面的数比后面的数大，刚交换
            if (arr[i] > arr[i + 1]) {
                temp = arr[i];
                arr[i] = arr[i + 1];
                arr[i + 1] = temp;
            }
        }
        System.out.println("第二趟排序后的数组："); //[-1, 3, -2, 9, 10]
        System.out.println(Arrays.toString(arr));

        //第三趟排序，就是将第三大的数排在倒数第三位
        for (int i = 0; i < arr.length - 1 - 2; i++) {
            //如果前面的数比后面的数大，刚交换
            if (arr[i] > arr[i + 1]) {
                temp = arr[i];
                arr[i] = arr[i + 1];
                arr[i + 1] = temp;
            }
        }

        System.out.println("第三趟排序后的数组："); //[-1, -2, 3, 9, 10]
        System.out.println(Arrays.toString(arr));

        //第四趟排序，就是将第四大的数排在倒数第四位
        for (int i = 0; i < arr.length - 1 - 3; i++) {
            //如果前面的数比后面的数大，刚交换
            if (arr[i] > arr[i + 1]) {
                temp = arr[i];
                arr[i] = arr[i + 1];
                arr[i + 1] = temp;
            }
        }

        System.out.println("第四趟排序后的数组："); //[-2, -1, 3, 9, 10]
        System.out.println(Arrays.toString(arr));*/

    }

    //不需要再进行第五趟排序
    //发现这四次for循环只有length-数字 不一样 ---->总结 length-i-1
    //封装到一个方法中
    //冒泡排序时间复杂度为O(n^2)
    //将冒泡排序封装到一个方法
    public static void bubbleSort(int[] arr) {
        int temp = 0;
        boolean flag = false; //标识变量，表示是否进行过交换
        for (int i = 0; i < arr.length - 1; i++) {
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    flag = true;
                    temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
            //System.out.println("第" + (i + 1) + "趟排序后的数组");
            //System.out.println(Arrays.toString(arr));
            if (!flag) { //在一趟排序中，一趟都没有交换过
                break;
            } else {
                flag = false; //重置flag，进行下次判断
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
  • 结果
排序前：
[3, 9, -1, 10, -2]
排序后：
[-2, -1, 3, 9, 10]
排序前的时间=：2022-12-30 21:30:36
排序后的时间=：2022-12-30 21:30:46

Process finished with exit code 0
1
2
3
4
5
6
7
8

# 选择排序

# 基本介绍

选择式排序也属于内部排序法，是从欲排序的数据中，按指定的规则选出某元素，再依规定交换位置后达到排序的目的。

# 选择排序思想

选择排序(select sorting)也是一种简单的排序方法。它的基本思想是:第一次从 arr[0]~arr[n-1]中选取最小值，与 arr[0]交换，第二次从 arr[1]~arr[n-1]中选取最小值，与 arr[1]交换，第三次从ar[2]~arr[n-1]中选取最小值，与ar[2]交换，…，第i次从 arr[i-1]~arr[n-1]中选取最小值，与arr[i-1]交换，…第n-1次从arr[n-2]~arr[n-1]中选取最小值，与arr[n-2]交换，总共通过n-1次，得到一个按排序码从小到大排列的有序序列。

# 选择排序思路分析图

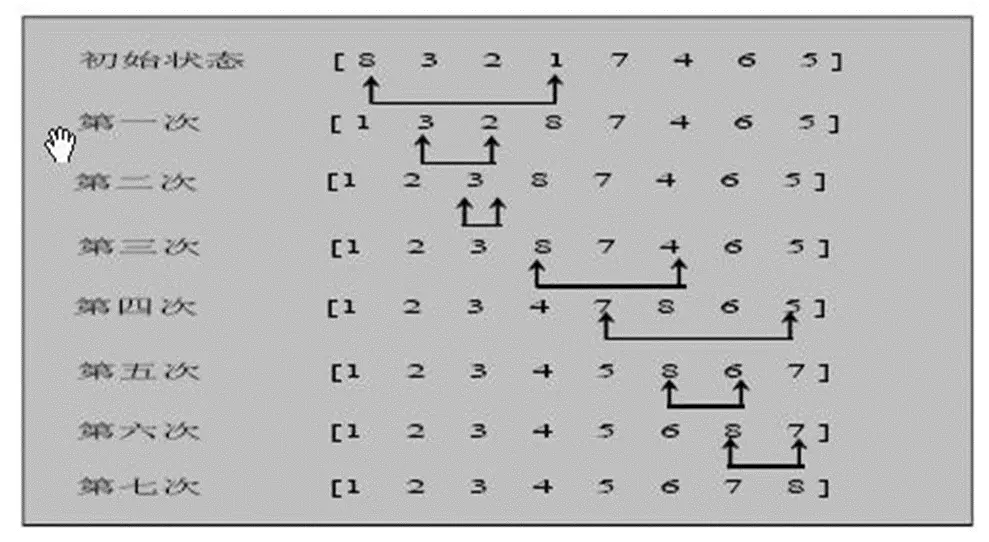
image

image

# 选择排序应用实例

有一群牛﹐颜值分别是10,34,1,19请使用选择排序从低到高进行排序[10,34,1,19]

image

  • 代码实现
/**
 * @author frx
 * @version 1.0
 * @date 2023/1/1  14:40
 * desc:选择排序
 */
public class SelectSort {
    public static void main(String[] args) {
        int arr[] = {10, 34, 1, 19};
        selectSort(arr);
        System.out.println(Arrays.toString(arr));
        //测试一下选择排序的速度,给80000个数据
        //创建要给80000个随机的数组
        int[] array = new int[80000];
        for (int i = 0; i < 80000; i++) {
            array[i] = (int) (Math.random() * 8000000); //生成一个[0,8000000)数
        }
        Date date1 = new Date();
        SimpleDateFormat dateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        String startTime = dateFormat.format(date1);
        System.out.println("排序前的时间=：" + startTime);

        selectSort(array);
        Date date2 = new Date();
        String endTime = dateFormat.format(date2);
        System.out.println("排序后的时间=：" + endTime);
    }

    //选择排序
    //每一轮排序都把最小的放到最前面，把最小的放在第0位，把第二小的放在第1位，把第三小的放在第2位...
    //需要arr.length-1次排序
    public static void selectSort(int[] arr) {

        //使用逐步推导的方式
        for (int i = 0; i < arr.length - 1; i++) {
            int minIndex = i;
            int min = arr[i];
            for (int j = i + 1; j < arr.length; j++) {
                if (min > arr[j]) {
                    min = arr[j];
                    minIndex = j;
                }
            }
            if (minIndex != i) {
                //将最小值，放在arr[i]，即交换
                arr[minIndex] = arr[i];
                arr[i] = min;
            }
        }

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
  • 结果
[1, 10, 19, 34]
排序前的时间=：2023-01-01 19:33:31
排序后的时间=：2023-01-01 19:33:34

Process finished with exit code 0
1
2
3
4
5

# 插入排序

# 基本介绍

插入式排序属于内部排序法，是对于欲排序的元素以插入的方式找寻该元素的适当位置，以达到排序的目的。

# 插入排序思想

插入排序(Insertion Sorting)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表，开始时有序表中只包含一个元素，无序表中包含有n-1个元素，排序过程中每次从无序表中取出第一个元素，把它的排序码依次与有序表元素的排序码进行比较，将它插入到有序表中的适当位置，使之成为新的有序表。

# 插入排序思路分析图

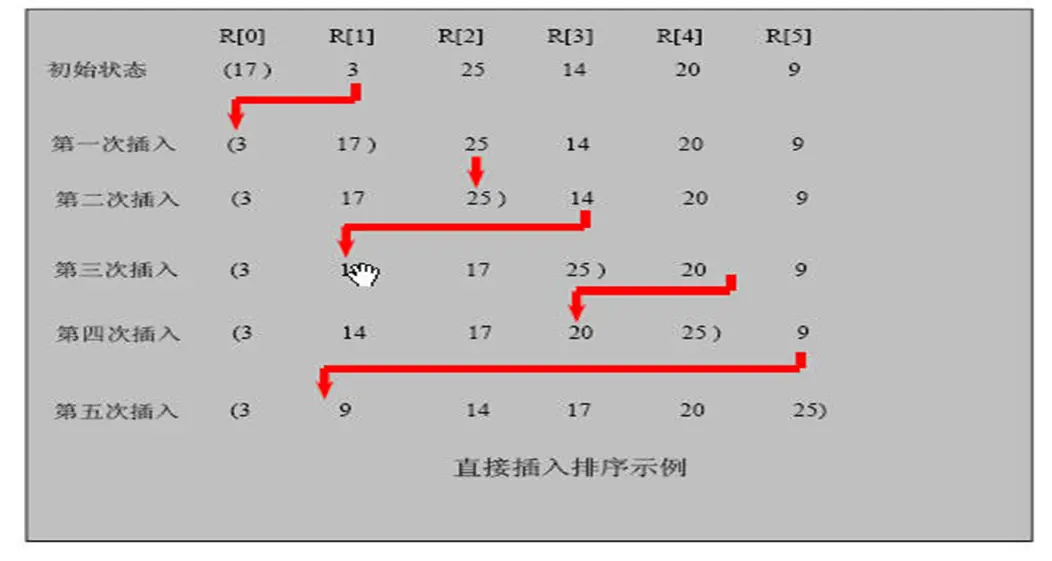
image

# 选择排序应用案例

有一群小牛，考试成绩分别是 101,34,119,1请从小到大排序

/**
 * @author frx
 * @version 1.0
 * @date 2023/1/1  20:34
 * desc:插入排序
 */
public class InsertSort {
    public static void main(String[] args) {
        int[] arr = {101, 34, 119, 1, 61, 89};
        insertSort(arr);
        System.out.println(Arrays.toString(arr));
        //测试一下选择排序的速度,给80000个数据
        //创建要给80000个随机的数组
        int[] array = new int[80000];
        for (int i = 0; i < 80000; i++) {
            array[i] = (int) (Math.random() * 8000000); //生成一个[0,8000000)数
        }
        Date date1 = new Date();
        SimpleDateFormat dateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        String startTime = dateFormat.format(date1);
        System.out.println("排序前的时间=：" + startTime);

        insertSort(array);
        Date date2 = new Date();
        String endTime = dateFormat.format(date2);
        System.out.println("排序后的时间=：" + endTime);
    }

    //插入排序
    public static void insertSort(int[] arr) {
        //第一轮 {101, 34, 119, 1} ==> {34, 101, 119, 1}

        int insertValue = 0;
        int insertIndex = 0;
        for (int i = 1; i < arr.length; i++) {
            //定义待插入的数
            insertValue = arr[i];
            insertIndex = i - 1; //即arr[i]的前面这个数的下标

            //给insertValue 找到插入的位置
            //说明
            //1.insertIndex >= 0 保证在给insertValue 找插入位置时，不越界
            //2.insertValue < arr[insertIndex] 待插入的数，还没有找到插入的位置
            //3.就需要将 arr[insertIndex] 值后移
            while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
                arr[insertIndex + 1] = arr[insertIndex];
                insertIndex--;
            }
            //直到插入的数不比前面的数小并且插入的索引大于等于0
            //就退出while循环，说明插入的位置找到，insertIndex + 1
            arr[insertIndex + 1] = insertValue;

            //System.out.println("第" + i + "轮插入");
            //System.out.println(Arrays.toString(arr));
        }

        //第2轮
        /*insertValue = arr[2];
        insertIndex= 2 - 1;
        while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
            arr[insertIndex + 1] = arr[insertIndex];
            insertIndex--;
        }
        //当退出while循环时，说明插入的位置找到，insertIndex + 1
        arr[insertIndex + 1] = insertValue;
        System.out.println("第二轮插入");
        System.out.println(Arrays.toString(arr));

        //第3轮
        insertValue = arr[3];
        insertIndex= 3 - 1;
        while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
            arr[insertIndex + 1] = arr[insertIndex];
            insertIndex--;
        }
        //当退出while循环时，说明插入的位置找到，insertIndex + 1
        arr[insertIndex + 1] = insertValue;
        System.out.println("第三轮插入");
        System.out.println(Arrays.toString(arr));*/

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
  • 结果
[1, 34, 61, 89, 101, 119]
排序前的时间=：2023-01-01 22:38:48
排序后的时间=：2023-01-01 22:38:49

Process finished with exit code 0
1
2
3
4
5

# 希尔排序

# 简单插入排序存在的问题

我们看简单的插入排序可能存在的问题.

数组arr = {2,3,4,5,6,1}这时需要插入的数1(最小),这样的过程是:

{2,3,4,5,6,6}

{2,3,4,5,5,6}

{2,3,4,4,5,6}

{2,3,3,4,5,6}

{2,2,3,4,5,6}

{1,2,3,4,5,6}

结论：当需要插入的数是较小的数时，后移的次数明显增多，对效率有影响.

# 希尔排序算法介绍

希尔排序是希尔〈Donald ShelI）于1959年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序。

# 希尔排序算法基本思想

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序;随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

# 希尔排序算法的示意图

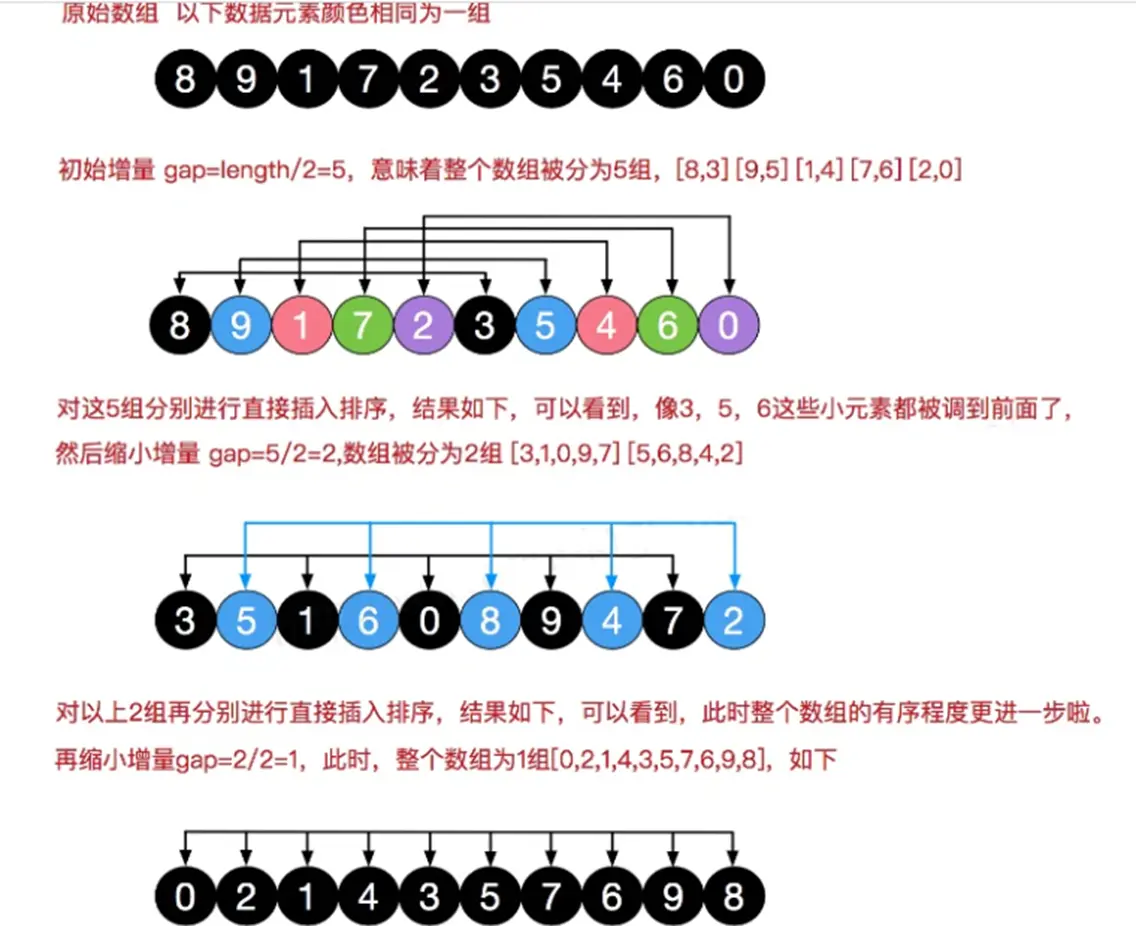
image

经过上面的“宏观调控”，整个数组的有序化程度成果喜人。

此时，仅仅需要对以上数列简单微调，无需大量移动操作即可完成整个数组的排序。

image

# 希尔排序应用案例

有一群小牛，考试成绩分别是 {8,9,1,7,2,3,5,4,6,0}请从小到大排序.请分别使用

希尔排序时，对有序序列在插入时采用交换法,并测试排序速度.

希尔排序时，对有序序列在插入时采用移动法，并测试排序速度

/**
 * @author frx
 * @version 1.0
 * @date 2023/1/2  14:03
 * desc:希尔排序
 */
public class ShellSort {
    public static void main(String[] args) {
        int[] arr = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0};
        System.out.println(Arrays.toString(arr));
        int[] array = new int[80000];
        for (int i = 0; i < 80000; i++) {
            array[i] = (int) (Math.random() * 8000000); //生成一个[0,8000000)数
        }
        Date date1 = new Date();
        SimpleDateFormat dateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        String startTime = dateFormat.format(date1);
        System.out.println("交换希尔排序前的时间=：" + startTime);

        shellSort(array);
        Date date2 = new Date();
        String endTime = dateFormat.format(date2);
        System.out.println("交换希尔排序后的时间=：" + endTime);

        int[] array1 = new int[80000];
        for (int i = 0; i < 80000; i++) {
            array1[i] = (int) (Math.random() * 8000000); //生成一个[0,8000000)数
        }

        Date date3 = new Date();
        String startTime2 = dateFormat.format(date3);
        System.out.println("移动希尔排序前的时间=：" + startTime2);

        shellSort2(array1);
        Date date4 = new Date();
        String endTime2 = dateFormat.format(date4);
        System.out.println("移动希尔排序后的时间=：" + endTime2);
    }

    //使用逐步推导的方式来编写希尔排序
    public static void shellSort(int[] arr) {

        int temp = 0;
        //根据逐步分析，得到循环处理
        for (int gap = arr.length / 2; gap > 0; gap /= 2) {
            for (int i = gap; i < arr.length; i++) {
                //遍历各组中所有的元素(共5组，每组有2个元素)，步长为gap
                for (int j = i - gap; j >= 0; j -= gap) {
                    //如果当前元素大于加上步长后的那个元素，说明交换
                    if (arr[j] > arr[j + gap]) {
                        temp = arr[j];
                        arr[j] = arr[j + gap];
                        arr[j + gap] = temp;
                    }
                }
            }
        }

        arr = new int[]{8, 9, 1, 7, 2, 3, 5, 4, 6, 0};
        //希尔排序的第1轮排序
        //因为第1轮排序，是将10个数据分成了5组
        for (int i = 5; i < arr.length; i++) {
            //遍历各组中所有的元素(共5组，每组有2个元素)
            for (int j = i - 5; j >= 0; j -= 5) {
                //如果当前元素大于加上步长后的那个元素，说明交换
                if (arr[j] > arr[j + 5]) {
                    temp = arr[j];
                    arr[j] = arr[j + 5];
                    arr[j + 5] = temp;
                }
            }
        }
        System.out.println("希尔排序1轮后=" + Arrays.toString(arr));

        //希尔排序第二轮排序
        //因为第2轮排序，是将10个数据分成了5/2 = 2组
        for (int i = 2; i < arr.length; i++) {
            for (int j = i - 2; j >= 0; j -= 2) {
                if (arr[j] > arr[j + 2]) {
                    temp = arr[j];
                    arr[j] = arr[j + 2];
                    arr[j + 2] = temp;
                }
            }
        }
        System.out.println("希尔排序2轮后=" + Arrays.toString(arr));

        //希尔排序第二轮排序
        //因为第2轮排序，是将10个数据分成了2/2 = 1组
        for (int i = 1; i < arr.length; i++) {
            for (int j = i - 1; j >= 0; j -= 1) {
                if (arr[j] > arr[j + 1]) {
                    temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
        System.out.println("希尔排序3轮后=" + Arrays.toString(arr));
    }

    public static void shellSort2(int[] arr) {
        for (int gap = arr.length / 2; gap > 0; gap /= 2) {
            //从gap个元素，逐个对其所在的组进行直接插入排序
            for (int i = gap; i < arr.length; i++) {
                int j = i;
                int temp = arr[j];
                while (j - gap >= 0 && temp < arr[j - gap]) {
                    //移动
                    arr[j] = arr[j - gap];
                    j -= gap;
                }
                //当退出while后，就给temp找到插入的位置
                arr[j] = temp;
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
  • 测试
[8, 9, 1, 7, 2, 3, 5, 4, 6, 0]
交换希尔排序前的时间=：2023-01-03 13:24:20
希尔排序1轮后=[3, 5, 1, 6, 0, 8, 9, 4, 7, 2]
希尔排序2轮后=[0, 2, 1, 4, 3, 5, 7, 6, 9, 8]
希尔排序3轮后=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
交换希尔排序后的时间=：2023-01-03 13:24:25
移动希尔排序前的时间=：2023-01-03 13:24:25
移动希尔排序后的时间=：2023-01-03 13:24:25

Process finished with exit code 0
1
2
3
4
5
6
7
8
9
10

# 快速排序

# 基本介绍

快速排序(Quicksort）是对冒泡排序的一种改进。基本思想是:通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

# 快速排序法示意图

image

image

# 快速排序法应用案例

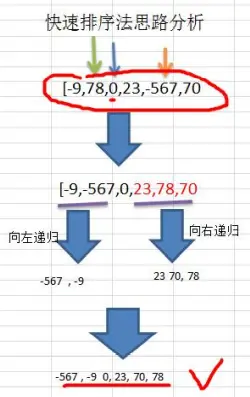
要求:对[-9,78,0,23,-567,70]进行从小到大的排序，要求使用快速排序法。【测试8w 和 800w】

说明[验证分析]:

  1. 如果取消左右递归，结果是 -9 -567 0 23 78 70
  2. 如果取消右递归,结果是 -567 -90 23 78 70
  3. 如果取消左递归,结果是 -9 -567 0 23 70 78
/**
 * @author frx
 * @version 1.0
 * @date 2023/1/3  16:39
 * desc: 快速排序
 */
public class QuickSort {
    public static void main(String[] args) {
        int[] arr = {-9, 78, 0, 23, -567, 70};
        quickSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));

        //测试一下快速排序的速度,给80000个数据
        //创建要给80000个随机的数组
        int[] array = new int[80000];
        for (int i = 0; i < 80000; i++) {
            array[i] = (int) (Math.random() * 8000000); //生成一个[0,8000000)数
        }
        Date date1 = new Date();
        SimpleDateFormat dateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        String startTime = dateFormat.format(date1);
        System.out.println("排序前的时间=：" + startTime);

        //测试快速排序
        quickSort(array, 0, array.length - 1);
        Date date2 = new Date();
        String endTime = dateFormat.format(date2);
        System.out.println("排序后的时间=：" + endTime);
    }

    public static void quickSort(int[] arr, int left, int right) {

        int l = left;//左边下标
        int r = right;//右边下标
        //pivot 中轴值
        int pivot = arr[(left + right) / 2];
        int temp = 0;//临时变量，作为交换时使用
        //while循环的目的是让比 pivot 值小的放到它的左边
        //比 pivot 值大的放到右边
        while (l < r) {

            //在 pivot 的左边一直找，找到大于等于 pivot 的值，才推出
            while (arr[l] < pivot) {
                l += 1;
            }
            //在 pivot 的右边一直找，找到小于等于 pivot 的值，才推出
            while (arr[r] > pivot) {
                r -= 1;
            }
            //如果 l>=r 成立说明 pivot 的左右两边的值，已经按照左边全部是
            if (l >= r) {
                break;
            }
            //交换
            temp = arr[l];
            arr[l] = arr[r];
            arr[r] = temp;

            //如果交换完后，发现这个arr[l] == pivot 值相等 r--，前移
            if (arr[l] == pivot) {
                r -= 1;
            }
            //如果交换完后，发现这个arr[r] == pivot 值相等 l++，后移
            if (arr[r] == pivot) {
                l += 1;
            }

        }

        //如果l==r，必须l++,r--，否则会出现栈溢出
        if (l == r) {
            l += 1;
            r -= 1;
        }

        //向左递归
        if (left < r) {
            quickSort(arr, left, r);
        }

        //向右递归
        if (right > l) {
            quickSort(arr, l, right);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
  • 结果
[-567, -9, 0, 23, 70, 78]
排序前的时间=：2023-01-08 21:11:09
排序后的时间=：2023-01-08 21:11:09

Process finished with exit code 0
1
2
3
4
5
#数据结构
上次更新: 2024/04/18, 13:08:42
递归
计算机网络-概述

← 计算机网络-概述→

最近更新
01
微信支付功能的实现与流程
11-21
02
购物车与结算区域的深入优化与功能完善
11-21
03
购物车与结算区域的功能实现与优化
11-21
更多文章>
Theme by Vdoing | Copyright © 2023-2024 EmmmuaCode | 黔ICP备2022009864号-2